GROWING TOWER-Shalini

I’m Shalini
GROWING TOWER


Florian Gorlitz, 22-year-old, German guy, who study biophysics, has created several experimental structures inspired from nature, combining with physics. He is an intelligent guy, playing with numbers and making extraordinary architectural structures. The growing tower is one of his many projects.
Brief
The idea was to build a 50’ tall tower with bamboo and thereby exhibiting the strength of bamboo. This was also designated to accommodate a living space on the platforms of it. the designing involved use of Fibonacci numbers and golden ratio.

Concept
The concept of the tower was inspired from plants and the technique of putting their leaves and branches and other parts of it. Plants are complex structures, changing their shapes in response to environmental factors such as sunlight, water and neighbouring plants. However, some mathematical rules can be found in their growth patterns, one of which is the golden section. The golden section can be observed in branching systems, phyllotaxis, flowers and seeds, and often the spiral arrangement of plant organs.
Although trees and bushes differ in shape, their ratio of length to width is close to the golden section. In some plant stems, the divergence angle between two adjacent leaves approximates 137.5°. This is the central angle forming two radii, and if we divide the circumference into two parts, the ratio is 1:0.618. This angle promotes adequate ventilation of the plants and is the optimal arrangement for light absorbance. Numbers of leaves, petals and fruiting bodies in some plants follow the sequence of Fibonacci numbers. This magical proportion is almost omnipresent, and is an essential feature of plants. It has great significance in biology and is also a common phenomenon within the growth and evolutionary processes of plants.


What is golden ratio?
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities.
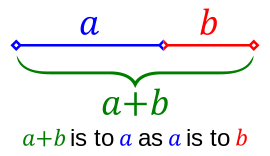
The Golden Ratio (also known as the Golden Section, Golden Mean, Divine Proportion or Greek letter Phi) exists when a line is divided into two parts and the longer part (a) divided by the smaller part (b) is equal to the sum of (a) + (b) divided by (a), which both equal 1.618.
What is Fibonacci numbers?
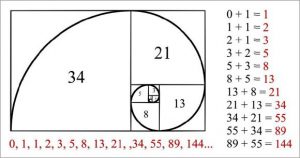
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number after the first two is the sum of the two preceding ones.
1,1,2,3,5,8,13,21,34,55,89,144….
They also appear in biological settings, such as branching in trees, phyllotaxis (the arrangement of leaves on a stem), the fruit sprouts of a pineapple, the flowering of an artichoke, an uncurling fern and the arrangement of a pine cone’s bracts.

Construction
The tower starts from a point on the ground, say 0. The tower grows from this point.

The next point, 1, is taken at an angle of 137.5*, also known as the golden angle. Now this point becomes the reference point to mark the next point at the same angle. This repeats itself and by joining these points, we build the whole tower.
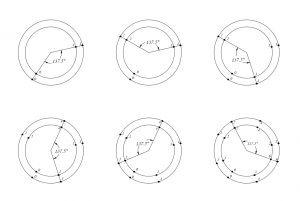
The tower is made as a combination of 3 smaller towers. The inner one having a radius of 1.57 meters ,the intermediate tower having a radius of 2.5 meters and the outer tower extending to a radius of 4.04 meters .The radii are obtained by multiplying the inner radius with 1.618, which is the golden ratio.

The construction is made of only isosceles triangles. But the two lengths are in a certain ratio together. To start with, the triangles on the inner tower has 2 members of length 1.476 and a shorter member of length 1.22 The same triangles are rotated to create the whole pattern of the inside tower. The same ratios are used to create the triangular modules that constitute the tower. Three lengths or more can be used. But the corner points of the triangles always mark points of the “golden angle”. The spiral appears by connecting every 3rd, 5th and 8th point of the tower.
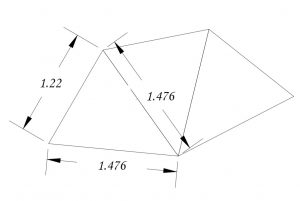
The length of the members of triangles in the three towers vary. But they are always in the ratio. These triangles are rotated and repeated to create the towers.

The foundation is built by digging soil 2’ deep and then inserting a stone pillar support the full length and then the bamboos are inserted to a depth of 1’ with a plastic bottle covering the inserted part to protect it from termites and decay.

The bamboos are joined at the junctions using junction clamps. Upto 6 bamboos can be inserted into the clamp.this enables smooth joints in the tower. The bamboos are then screwed in throught the clamp after insertion.

There are 2 platforms in the tower. The distance between the 2 platforms is 4.2 meters and the distance from the 2nd platform to the dome is 2.6 meters. The platforms are made of coconut tree trunk planks.

The dome is the extension of the intermediate tower built by triangles but of different sizes.

Estimation
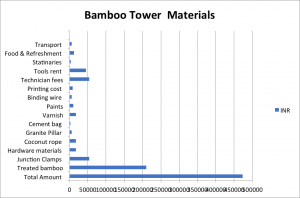
| Treated Bamboo | Junction Clamps | Hardware material | Coconut rope | Granite pillar | Cement bag | Varnish | Paints | Binding wire | Printing | |
|
Amount |
210000 |
54000 |
18000 |
18000 |
6000 |
3000 |
18000 |
11000 |
6000 |
9000 |
| Technician fees | Tools rent | Stationaries | Food and refreshment | Transport | Total | ||
|
Amount |
54000 |
45000 |
3600 |
12000 |
6000 |
473600 |
|
Structural analysis
Structurally analysing the tower, as much it feels stable from bottom, so much does it sways at the top. This from my analysis of the tower can be due to the remaining unsupported height of the tower. This can be rectified by connecting 3 steel cable of 20mm diameter, to the tower, which are inserted in the ground and having a length of 14.5 meters. This will make the whole structure more stable. This could also have been achieved if the outermost tower is increased in height.
The coconut planks used for the platforms are soft and hence it doesn’t have so much of strength and decays quick as it is exposed to direct weather conditions. These planks are also heavier and hence add on to the total load the tower should carry. Use of low weight, long lasting wood can help solve this problem.
The whole tower is made up of treated bamboo but the bamboos are not varnished or treated to protect it from climatic conditions. Direct exposure to sunlight rain and other climatic factors contribute to fast deterioration of the stucture. Varnishing of the tower or any other treatment to externally protect it from weather would also help.
Conclusion
This tower is an example of most stable way to build domes and towers. The helix structure can also withstand earthquakes. Even if one element is broken, the structure is stable and does not crash down. This also depicts the structural stability of bamboo and its high tensile strength. The growing tower is also the result of continues hard work by all the volunteers who worked as a team, putting their blood and sweat into it. This tower design can be replicated and used for several purposes.
The tower can be used for multiple purposes from watertank to mobiletower to space for accomodation. This can be achieved only by making the strucutre more stable and calculating the load to be carried by the tower for several purposes and exploring the design accordingly.




Leave a comment